Swin Transformer
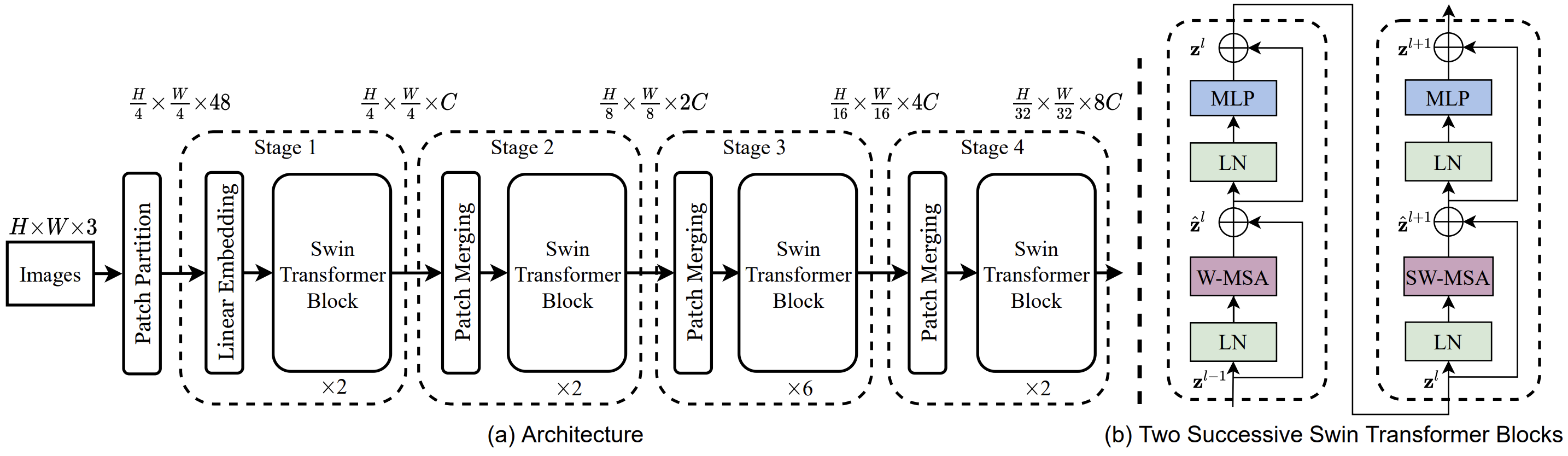
Swin-Transformer在Transformer模块中使用了类似于深度卷积网络的“层次化构建”方法,引入“Patch”的概念,同时修改了网络的Block
在开始前,Swin-Transformer首先对输入图像做一次Patch Partition+Patch Embedding,之后送入BackBone中。在BackBone里,Feature Map的尺寸逐渐减小,感受野逐渐扩大;同时在一个Block里,Feature Map被一个个Patch分割
注意,(b)中结构是成对出现的,所以Block的重复次数一定是偶数,它们的Attention模块不同
1. Patch Partition
input = (H, W, 3),output = (H/4, W/4, 3*16=48),易得Patch Partition是将输入图像做4x4的Patch分割,每张RGB图像有3通道,即得到了48个(H/4, W/4)大小的输入
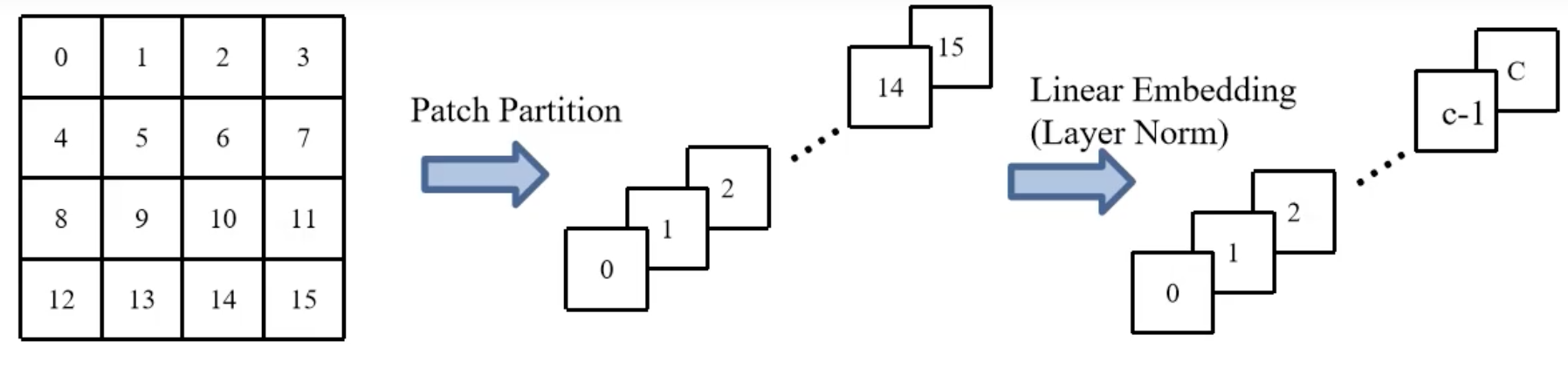
2. Linear Embedding
通过一层stride = kernel_size的卷积层实现,input = (H/4, W/4, 48),output = (H/4, W/4, C),这里的C由网络的不同版本类型指定
3. Patch Merging
如下图,在CNN中,我们通过池化操作来下采样;Swin-Transformer中的Patch Merging操作是将Feature Map分成无数个4x4的Patch,分别提取每个Patch的[0, 0]、[1, 0]、[0, 1]、[1, 1]位置作为新的channel,这样实现尺寸变为原来四分之一,但通道数翻4倍
这样的好处是可以进行不同window之间的shuffle操作,使得后续的W-MSA、SW-MSA可以实现不同window的信息交流

然后再通过Layer Norm,最后接一个Conv1x1将channel再次减半
4. W-MSA
即Windows - Multi-head Self-Attention模块,将特征图分成若干个window,对每个window进行Self-Attention,减小计算量
5. SW-MSA
即Shifted Windows - Multi-head Self-Attention模块。为了解决W-MSA中信息交互问题,作者提出通过Shift偏移方式,即将图像向右下偏移$\frac{window_size}{2}$个单位,如下图,则区域自左到右、自上而下被划分为A1、C1、A2、B1、D、B2、A3、C2、A4。此时B、C包含了2个window的信息,D包含了4个window
但这样,显然不方便计算。因此我们移动新划分的区域,如下图,即可实现新的窗口划分,这样每个window的尺寸就相同了
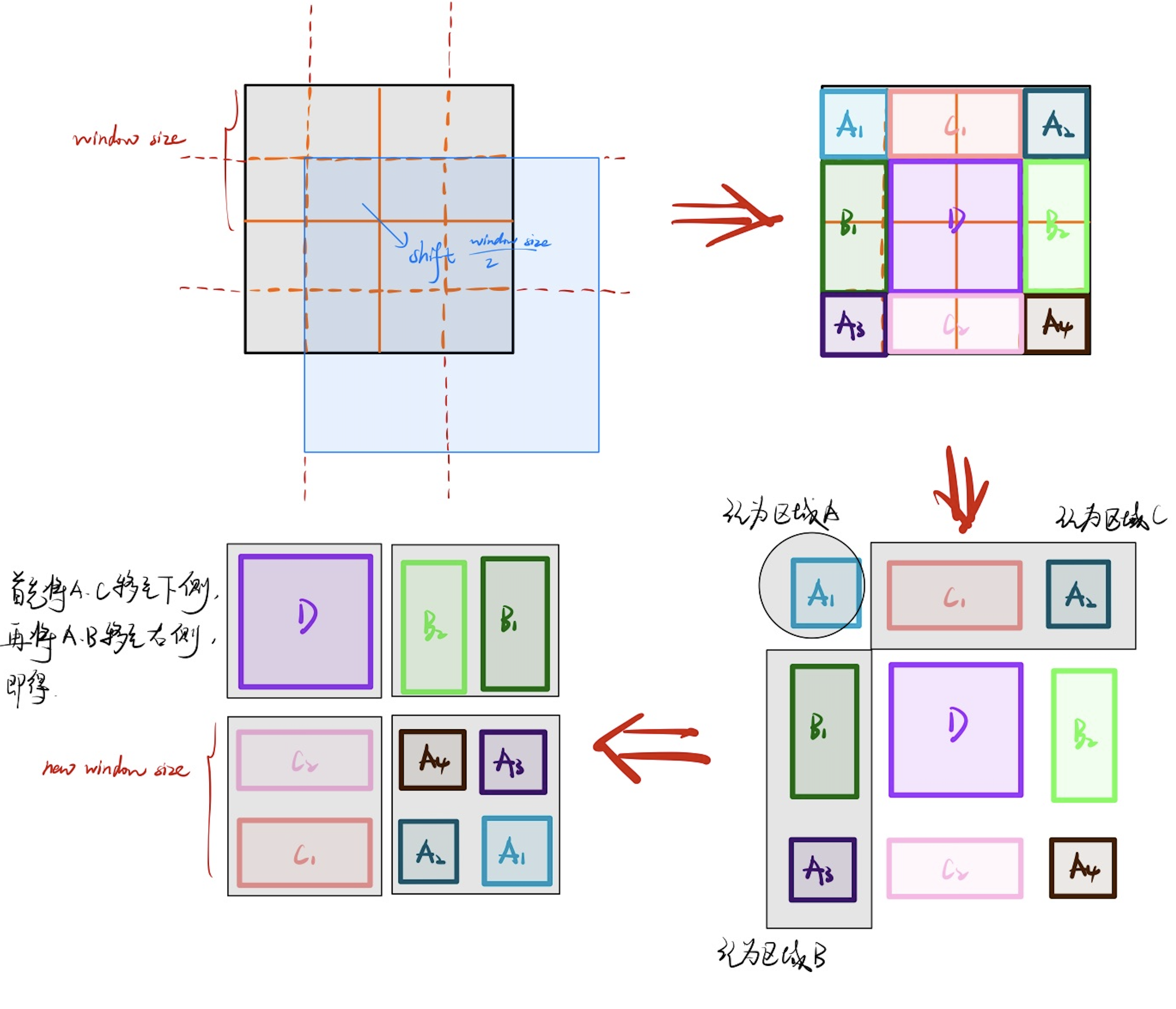
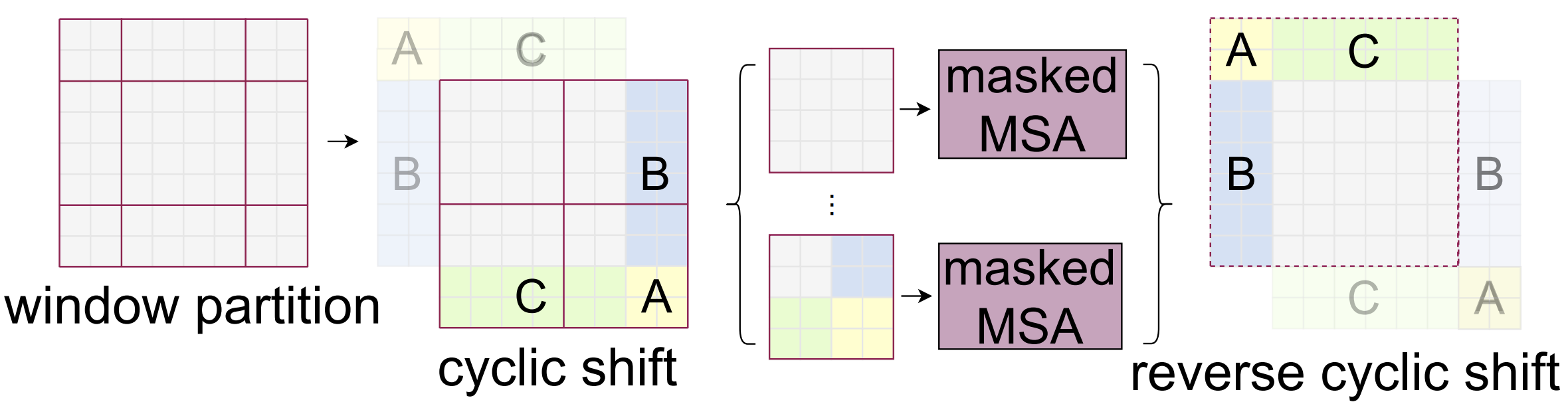
而为了计算时B1、B2互不干扰,C1、C2互不干扰,因此在每个MSA中做mask操作。掩码操作同Transformer中Decoder的操作,对于对应掩码位置直接减去一个INF(无穷大),则softmax后这里就置零了。如果忘记了请移步:
6. Relative Position Bias
就是在Attenton中添加了位置偏移信息,具体是通过MLP的bias实现,效果很玄学,公式如下:
$$
Attention=SoftMax(\frac{QK^T}{\sqrt{d}}+B)V
$$
Note:w/o是without的缩写,w/是with的缩写
关于偏置B是如何实现的,见下文:
如图所示,对于位置在$(x_0,\ y_0)$的像素,它的绝对位置编码就是它本身的坐标,它关于$(x_1,\ y_1)$的相对位置坐标是$(x_0-x_1,\ y_0-y_1)$
则对于尺寸为$window\text{_}size$的窗口,每个位置都有对应的$window\text{_}size-1$个相对位置编码,将其拉成1维,重复计算其他位置可得如下$shape=(window\text{_}size, window\text{_}size)$的Relative Position Table,Relative Position Table[window_size *x+y][:]是$(x,y)$位置关于其他位置的相对位置编码

现在的问题是,如何去索引第二维,进而取出偏置?关于位置$(x_0,y_1)、(x_1, y_0)$,若直接两维相加,则映射在一维是等价的,实际二者的偏置信息存储在不同位置
首先需要将每个维度加上$window\text{_}size-1$,以保证偏移量从0开始(对于$size=window\text{_}size$大小的窗口,最小偏移量就是$-window\text{_}size+1$)
然后对第一维做处理,对第一维乘以2倍的窗口大小减1,再进行两个维度的相加。这样就不会出现相同值的情况了,这样就得到了位置索引表
根据这张表,可以很方便的索引到一维的Relative Position Table表,该表是一张一维表,大小是$(2 * window\text{_}size-1)^2$。因为对于上述索引表,原始的最大偏置量即$2 * window\text{_}size - 2$,则可以计算最大一维映射偏置量为:
$$(2 * window\text{_}size - 2) * (2 * window\text{_}size - 1) + 2 * window\text{_}size - 2 = (2 * window\text{_}size - 1)^2 - 1$$
则索引范围是$[0,(2*window\text{_}size-1)^2]$,即证